Published on: April 7, 2023
Written by Jonas Frank / Fact-checked by Nova Scarlett
In physics, the law of conservation of energy states that the total energy of an isolated system remains constant it is said to be conserved over time. This law is a direct consequence of the fact that the laws of physics are time-reversible. The total energy includes both kinetic energy and potential energy.
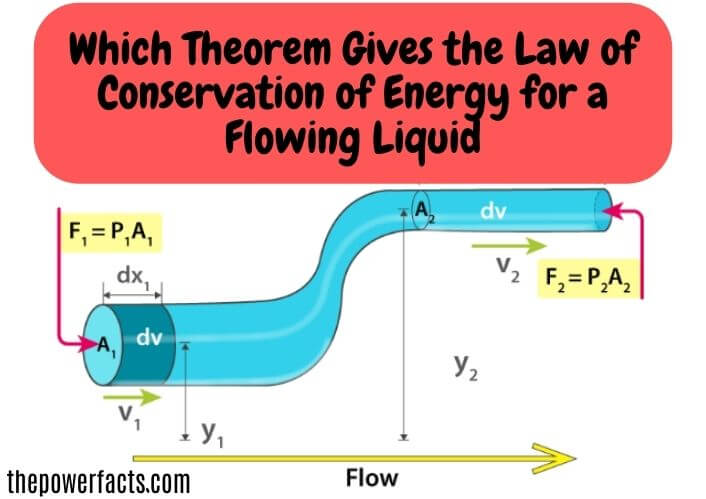
The theorem that gives the law of conservation of energy for a flowing liquid is the Bernoulli equation. This equation states that the sum of the kinetic energy, potential energy, and pressure energy in a fluid is constant. This principle can be applied to any moving fluid, whether it is a liquid or gas.
State Bernoulli’s Theorem And Prove It
In mathematics, Bernoulli’s theorem states that if two independent random variables X and Y are both distributed according to the same Bernoulli distribution with parameter p, then their sum Z = X + Y is also distributed according to a Bernoulli distribution with parameter p. In other words, the sum of two independent random variables is itself a random variable, and its distribution is determined by the parameter p. The theorem is named after Swiss mathematician Jakob Bernoulli, who proved it in his 1713 book Ars Conjectandi.
The result had been discovered earlier by English mathematician Isaac Newton. To prove the theorem, we first need to recall some basic properties of the Bernoulli distribution. If X is a random variable distributed according to the Bernoulli distribution with parameter p, then we say that X has a Binomial(1,p) distribution.
This means that X can take on only two values: 0 and 1, and that these values are equally likely if p = 0.5. The probability mass function of X is given by: P(X=0) = (1-p)
P(X=1) = p Now let’s suppose that X and Y are both distributed according to the same Bernoulli distribution with parameter p. We want to show that their sum Z = X + Y is also distributed according to a Bernoulli distribution with parameter p.
To do this, we need to calculate the probability mass function of Z. Recall that for any discrete random variable Z, its probability mass function P(Z=z) gives us the probability that Z takes on the value z. So we have: P(Z=0) = P((X+Y)=0)
= P((X=0)*(Y=0)) // since X and Y are independent = P(X=0)*P(Y=0) // using properties of independence = (1-p)*(1-p), // since each term has PMF (1-p).
Bernoulli Equation Derivation
The Bernoulli equation is a powerful tool that can be used to solve many problems in fluid mechanics. In this blog post, we will derive the Bernoulli equation and then use it to solve some simple problems. The Bernoulli equation is derived from the conservation of energy principle.
This principle states that the total energy of a system is conserved, or remains constant. For a fluid flowing through a pipe, the total energy consists of two components: pressure energy and kinetic energy. The pressure energy is due to the force exerted by the fluid on the walls of the pipe, and the kinetic energy is due to the motion of the fluid.
We can use calculus to show that the rate at which these two energies are lost (or gained) must be equal. This leads us to the Bernoulli equation: P + 1/2 ρ v^2 = constant.
Where P is pressure, ρ is density, and v is velocity. This equation states that for a given volume of fluid flowing through a pipe if the pressure decreases then either the velocity must increase or else the density must decrease (or both). Conversely, if either velocity or density increases, then pressure must decrease in order for total energy to remain constant.
Bernoulli’s Theorem
Bernoulli’s theorem is a statement in fluid dynamics that describes the relationship between pressure and velocity in a moving fluid. The theorem is named after Daniel Bernoulli, who published it in his book Hydrodynamica in 1738. The theorem states that for an inviscid flow of an incompressible fluid, the sum of the kinetic energy and the potential energy per unit volume is constant.
| Point 1 | This principle is often referred to as the law of conservation of energy. The Bernoulli equation can be derived from the principle of conservation of energy and applies to any inviscid, incompressible flow, whether steady or unsteady, laminar or turbulent. In fact, it is one of the most important equations in all of fluid mechanics. |
| Point 2 | The Bernoulli equation has many applications in engineering and physics. For example, it can be used to calculate the pressure drop across a valve or nozzle or to determine the lift force on an airfoil. It also forms the basis for understanding how blood flows through arteries and how air flows around an airplane’s wings. |
Bernoulli’s Theorem Application
In probability theory, Bernoulli’s theorem (also called the law of large numbers in Bernoulli’s form) is a result of sums of independent random variables. It is named after Jacob Bernoulli, who proved it in his work Ars Conjectandi.[1]
The theorem says that if X 1, and X 2, are independent random variables with mean μ 1, μ 2, and variance σ 1 2, σ 2 2 respectively, then as n → ∞, the sum of these random variables divided by n converges in distribution to a normal distribution with mean μ and variance σ2/n. In symbols: where Φ denotes the cumulative distribution function of the standard normal distribution.
Bernoulli’s Principle Example
In fluid dynamics, Bernoulli’s principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid’s potential energy. The principle is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738.
A simple example of Bernoulli’s principle is provided by the wing of an airplane.
As airspeed increases, the pressure on the top surface of the wing decreases relative to the bottom surface. This difference in pressure creates lift, which allows an airplane to fly.
State Bernoulli’s Theorem in Fluid Mechanics
In fluid mechanics, Bernoulli’s principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid’s potential energy. The principle is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738. The principle can be applied to various types of fluids, including incompressible and compressible fluids.
For incompressible fluids, such as water or air, the principle states that if the fluid is flowing along a curved path (such as through a pipe), there is a decrease in pressure at points where the speed of the fluid increases. This decrease in pressure is caused by an increase in the kinetic energy of the fluid at those points. Similarly, for compressible fluids (such as gases), an increase in speed occurs simultaneously with a decrease in density (and thus an increase in temperature).
Again, this change is due to an increase in kinetic energy. Bernoulli’s principle can be used to explain several interesting phenomena, such as how airplanes are able to fly and how blood flows through our arteries. In both cases, it is the decreases in pressure (or density) that allow objects to move against gravity – either by lifting them up into the air or by pushing them forward through our arteries.
Bernoulli’s Equation
In fluid dynamics, Bernoulli’s equation is a mathematical expression of the conservation of energy for fluids in motion. It states that the sum of the kinetic energy and the potential energy in a moving fluid remains constant. The equation is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738.
The Bernoulli equation can be applied to any moving fluid, including liquids, gases, or plasmas. It is derived from the principle of conservation of energy, which states that the total energy of a system must remain constant over time. In a flowing fluid, this requires that the sum of the kinetic energy and potential energy must be constant.
The Bernoulli equation has many applications in engineering and physics. For example, it can be used to predict how fluids will flow through pipes or around objects in a streamlined pattern. It can also be used to calculate the pressure exerted by a liquid on a container wall or the force exerted by a gas on an object in a wind tunnel.
FAQs
1. What Does Bernoulli’s Theorem State?
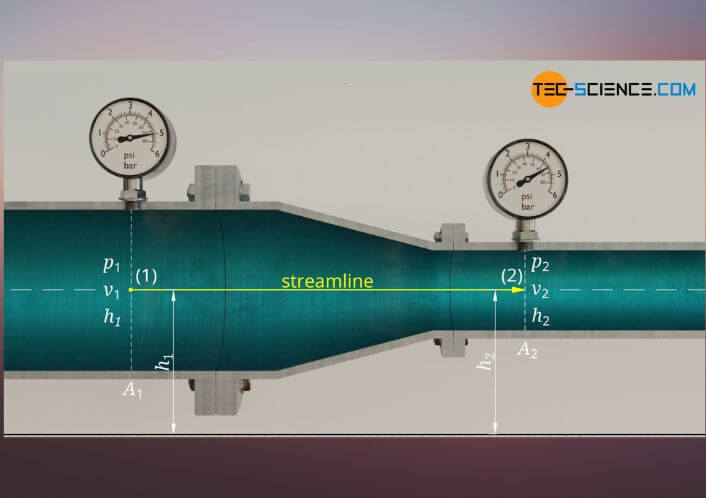
In fluid dynamics, Bernoulli’s equation is a mathematical expression of the conservation of energy for fluids moving along a streamline. The equation was first discovered by Swiss mathematician Daniel Bernoulli in 1738. The Bernoulli equation states that for an inviscid flow of a liquid, the sum of the kinetic energy and the potential energy per unit volume is constant along a streamline.
In other words, if you were to take a snapshot of a section of fluid at any point in time, the total energy per unit volume would be the same throughout that section. The Bernoulli equation can be applied to any incompressible fluid, including liquids and gases. In fact, it’s not even limited to fluids – it can also be used to describe the motion of objects through the air or other mediums where drag forces are present.
The Bernoulli equation has many applications in engineering and physics. For example, it can be used to calculate the lift force on an airplane wing or the pressure drop across a valve in a piping system. It’s also commonly used in analyzing blood flow through arteries and veins.
2. Which Conservation Law is Applicable to Bernoulli’s Theorem?
In physics, a conservation law states that the total value of some quantity is constant throughout time. This quantity can be mass, energy, momentum, electric charge, or another property of matter or spacetime. The best-known conservation laws are the laws of conservation of energy and momentum.
Bernoulli’s theorem is a statement in fluid dynamics that describes how the pressure and velocity of a moving fluid change as the fluid flows from one point to another. The theorem is named after Dutch physicist Daniel Bernoulli who published it in his book Hydrodynamica in 1738. The applicable conservation law to Bernoulli’s theorem is the law of conservation of energy.
This law states that energy cannot be created or destroyed; it can only be transformed from one form to another. In other words, the total amount of energy in the universe is always constant. Applying this law to Bernoulli’s theorem, we can see that the kinetic energy (energy associated with motion) of a moving fluid must be equal to its potential energy (energy associated with position).
As the fluid flows from one point to another, its potential energy decreases due to gravity while its kinetic energy increases due to the flow itself. Since Energy = Kinetic Energy + Potential Energy, this decrease in potential energy must be balanced by an increase in kinetic energy; otherwise, there would be a net loss or gain of energy which violates the law of conservation of energy.
3. Is Bernoulli’s Principle Conservation of Energy?
No, Bernoulli’s principle is not the conservation of energy. While both principles are concerned with the relationship between energy and fluid flow, they are different concepts. Bernoulli’s principle states that an increase in the speed of fluid results in a decrease in pressure.
This occurs because as the fluid moves faster, its molecules have less time to interact with each other, resulting in fewer collisions and less pressure. Conservation of energy, on the other hand, states that energy cannot be created or destroyed, only converted from one form to another. In the context of fluid flow, this means that the total amount of energy remains constant even as it changes form (e.g. from kinetic to potential).
So while Bernoulli’s principle can be used to explain how energy is transferred within a flowing fluid, it is not itself a law of conservation.
4. What is the Conservation of Energy in Fluid Flow?
In fluid flow, the conservation of energy states that the total energy of a system remains constant. The total energy includes both the kinetic and potential energies. The sum of these two energies is called mechanical energy.
In a closed system, such as a sealed container of water, the conservation of energy states that the mechanical energy is constant. The potential energy in fluid flow comes from the height difference between two points. The higher point has more potential energy because it has the ability to do work on objects below it.
The kinetic energy comes from the movement of the fluids themselves. In an open system, such as a river or waterfall, there is also thermal energy due to friction between the fluid and its surroundings. The conservation of energy is important because it helps us understand how systems work and how they will change over time.
It also helps engineers design better systems by understanding how much Energy is available to do work.
Understanding Bernoulli’s Equation
Last Point
The law of conservation of energy for a flowing liquid states that the total energy of the liquid is constant. This theorem is based on the fact that the total energy of a system cannot be created or destroyed, but only converted from one form to another. The theorem applies to both closed and open systems.
Read more:
